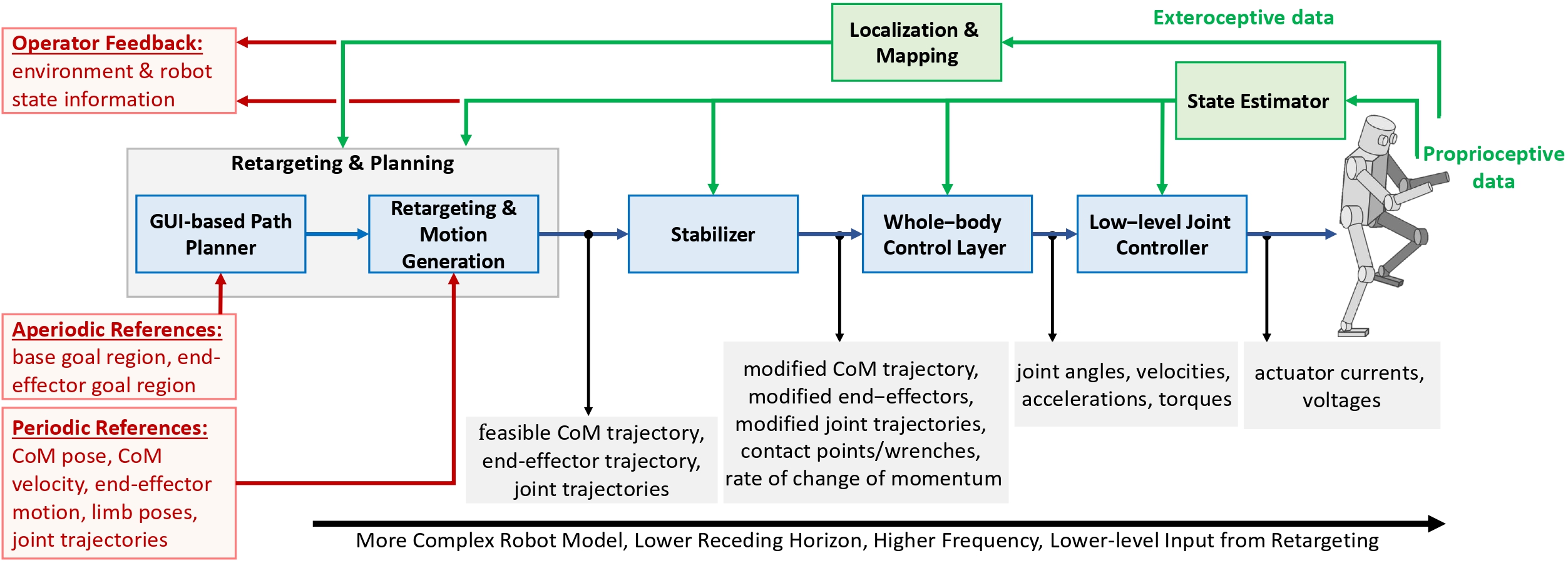
III. HUMANOID ROBOT RETARGETING & CONTROL

This section describes the retargeting and control techniques for unilateral teleoperation of humanoid robots. We can define the retargeting and control as a mapping \(\mathbb{H}: A \to A^{\prime}\) where \(A\) is the domain of the perceived human actions (kinematic and dynamic trajectories) and \(A^{\prime}\) is the space of robot actions. In this definition, the mapping principle identifies the robot autonomy and the human authority in the teleoperation scenario. This mapping should be identified such that it minimizes the difference between the human intent and the robot actions while respecting the constraints in the teleoperation scenario.

Humanoid robot retargeting and control introduces many challenges to teleoperation scenarios, namely due to the nonlinear, hybrid, and underactuated dynamics of humanoids with high degrees of freedom, as well as imprecise robot dynamical model and control, and partially-known environment dynamics. All these challenges together with the fact that the robot retargeting and controller blocks (in Fig. 3) usually run online, make the problem even more complicated. To overcome the introduced challenges, model-based optimal control architectures are the foremost technique used in the literature. During DRC, most of the finalist architectures converged to a similar design where the robot trajectories and stability are achieved by retargeting and control blocks connected in cascade. This architecture is conceptually demonstrated in Fig. 3, where its blocks are characterized in the following sections. This architecture needs a humanoid model (Sec.III-A), human references coming from teleoperation devices, and the robot environment information. Finally, challenges unique to humanoid robot retargeting, control, and possible future directions are discussed in Sec. III-G.

Fig. 3: Flowchart of a humanoid robot retargeting, planning, and control architecture (red color: references/feedback of human; blue color: retargeting, motion generation, and control; green color: perception and estimation).

A. Modeling

1) Notations and complete humanoid robot models

Most humans and humanoid robots are modeled as multi-body mechanical systems with \(n+1\) rigid bodies, called links, connected with \(n\) joints, each with one degree of freedom. The configuration of a humanoid robot with \(n\) joints depends on the robot shape, i.e., joint angles \(\bf{s}\in \mathbb{R}^n\), the position \(^{\mathcal{I}}\bf{p}_{\mathcal{B}}\in \mathbb{R}^3\), and orientation \(^{\mathcal{I}}{\bf{R}}_{\mathcal{B}}\in SO(3)\) of the floating base (usually associated with the pelvis, \({\mathcal{B}}\)) relative to the inertial or world frame \(\mathcal{I}\)\footnote{ With the abuse of notation, we will drop \(\mathcal{I}\) in formulas for simplicity.}. The robot configuration is indicated by \(\bf{q} = (^{\mathcal{I}}\bf{p}_{\mathcal{B}}, ^{\mathcal{I}}{\bf{R}}_{\mathcal{B}}, \bf{s})\). The pose of a frame attached to a robot link \(\mathcal{A}\) is computed via \((^{\mathcal{I}}\bf{p}_{\mathcal{A}}, ^{\mathcal{I}}\bf{R}_{\mathcal{A}}) = \bf{\mathcal{H}}_A(\bf{q})\), where \(\bf{\mathcal{H}}_A(\cdot)\) is the geometrical forward kinematics. The velocity of the model is summarized in the vector \(\bf{\nu}=(^{\mathcal{I}}\dot{\bf{p}}_{\mathcal{B}},^{\mathcal{I}}{\bf{\omega}}_{\mathcal{B}}, \dot{\bf{s}}) \in \mathbb{R}^{n+6}\), where \(^{\mathcal{I}}\dot{\bf{p}}_{\mathcal{B}}\), \(^{\mathcal{I}}{\bf{\omega}}_{\mathcal{B}}\) are the base linear and rotational (angular) velocity of the base frame, and \(\dot{\bf{s}}\) is the joints velocity vector of the robot. The velocity of a frame \(\mathcal{A}\) attached to the robot, i.e., \(^{\mathcal{I}}\bf{v}_{\mathcal{A}}= (^{\mathcal{I}}\dot{\bf{p}}_{\mathcal{A}},^{\mathcal{I}}{\bf{\omega}}_{\mathcal{A}})\), is computed by Jacobian of \(\mathcal{A}\) with the linear and angular parts, therefore \(^{\mathcal{A}}\bf{v}_{\mathcal{I}}= \bf{\mathcal{J}}_A(\bf{q}) \bf{\nu}\). Finally, the \(n+6\) robot dynamics equations, with all \(n_c\) contact forces applied on the robot, are described by : \begin{equation} \bf{M}(\bf{q}) \dot{\bf{\nu}} + \bf{C}(\bf{q},\bf{\nu})\bf{\nu} + \bf{g}(\bf{q}) = \bf{B}\bf{\tau} + \sum_{k=1}^{n_c}\bf{\mathcal{J}}_{k}^{T}(\bf{q}){\bf{f}^{c}_k} \end{equation} where \(\bf{M}(\bf{q})\) is the symmetric positive definite inertia matrix of the robot, \(\bf{C}(\bf{q},\bf{\nu})\) is the vector of Coriolis and centrifugal terms, \(\bf{g}(\bf{q})\) is the vector of gravitational terms, \(\bf{B}=(\bf{0}_{n\times{6}},\bf{1}_n)^T\) is a selector matrix, \(\bf{\tau}\) is the vector of actuator joint torques, and \(\bf{f}^{c}_{k}\) is the vector of the \(k\)-th contact wrenches acting on the robot. More information about the humanoid robot modeling can be found in .

2) Simplified humanoid robot models

Various simplified models are proposed in the literature in order to extract intuitive control heuristics and for real-time lower order motion planning. The most well-known approximation of humanoid dynamics is the inverted pendulum model . In this model, the support foot is connected through a variable-length link to the robot center of mass (CoM). Assuming a constant height for the inverted pendulum , one can derive the equation of motion of the Linear Inverted Pendulum Model (LIPM) by: \begin{equation} \ddot{\bf{x}} = \frac{g}{z_0}({\bf{x} - \bf{x}_{b}}), \label{eq:lipm} \end{equation} where \(g\) is the gravitational acceleration constant, \(z_0\) is the constant height of the CoM, \(\bf{x} \in \mathbb{R}^2\) is the CoM coordinate vector, and \(\bf{x}_{b} \in \mathbb{R}^2\) is the base of the LIPM coordinate vector.

The base of the LIPM is often assumed to be the Zero Moment Point (ZMP) (equivalent to the center of pressure, CoP) of the humanoid robot . The LIPM dynamics can be divided into stable and unstable modes, where the unstable mode is referred as (instantaneous) Capture Point , or Divergent Component of Motion (DCM) in the literature. The DCM dynamics is characterised by a first-order system as: \begin{equation} {\bf{\xi}} = \bf{x} + b{\bf{\dot{x}}}, \label{eq:dcmCOM} \end{equation} where \(\bf{\xi}\) and \(b = \sqrt{\frac{z_0}{g}}\) are the DCM variable and the time constant. Equation (3) shows that the CoM follows the DCM. Differentiating Eq. (3) and replacing into Eq. (2) results in: \begin{equation} \dot{\bf{\xi}} = \frac{1}{b} (\bf{\xi}- \bf{x}_b). \label{eq:dcm} \end{equation} Equations (3) and (4) together represent the LIPM dynamics.

B. Retargeting and Planning

The goal of this block in Fig. 3 is to morph the human commands or measurements coming from the teleoperation devices into robot references. It comprises the reference motions for the robot links as well as the robot locomotion references, i.e., alternate footstep locations, timings, and allocating a given footstep to the left or right foot to follow the user’s commands. The input to this block may vary according to the task and system requirements, and consequently the design choice and retargeting policy differ. Besides, the retargeting policy can even be determined online as a classification or regression problem using the human speech and psychophysiological state. For example in , the authors developed attentive systems for real-time adaptation of the retargeting policy and the robot autonomy level. As we go from the left to the right in Fig. 3, the level of automation and the input frequency increase, and higher communication bandwidth with lower delays is required. The approaches presented in this part are model-based, while learning-based techniques for retargeting will be discussed later in Sec. III-G.

Teleoperation devices may provide different types of input to retargeting and planning. The inputs can be i) the desired goal pose (region) in the workspace for the base and the end-effectors using GUIs (high-level), ii) the CoM velocity, the base rotational velocity, the end-effector motion, the user’s desired footstep contacts, or whole-body motion (low-level). While at a low-level, the user is in charge of the obstacle avoidance, the planning and retargeting at the high-level deals with finding the path leading to the desired goal. The output of the high-level goes to the lower level in order to finally compute the robot reference joint angles, footstep contacts and timings as the output of the block. We structured the rest of this subsection according to the input category.

1) GUI-based Path Planner

When the user provides the goal region of the robot base or arms through GUIs, the humanoid robot not only should plan its footsteps or arm motion but also should find a feasible path for reaching the goal, if any exists. Related to the footsteps, contrary to wheeled mobile robots, a feasible path here refers to an obstacle-free path or one where the humanoid robot can traverse the obstacles by stepping over. Primary approaches for solving the high-level path planning are search-based methods and reactive methods. The first step toward finding a feasible path, i.e., regions where the robot can move, is to perceive the workspace by means of the robot perception system. Following the identification of the workspace, a feasible path is planned.

Search-based algorithms try to find a path from the starting point to the goal region by searching a graph. The graph can be made using a grid map of the environment or by a random sampling of the environment. Some of the methods used in the literature to perform footstep planning are A* , D* Lite , RRT variations , and dynamic programming techniques . The completeness, global optimality, and the ability of real-time replanning of the path in dynamic environments are the important features of these search-based algorithms when selecting a proper method. These algorithms are not very efficient for real-time execution when an exhaustive search is done, hence, to enhance the efficiency a heuristic is chosen in order to prune the search space and perform a greedy search.

Reactive methods for high-level kinematic retargeting and path planning problems can be addressed as an optimization problem or as a dynamical system. In the problem has been tackled with a Model Predictive Control (MPC) approach. It allows finding the foot poses as a continuous decision-making problem by formulating it as a Quadratic Programming (QP) optimization problem. However, when the end-effector rotation or the obstacle-avoidance is added to the problem, the optimization problem becomes non-convex, therefore, there is no guarantee on completeness and global optimality . However, although there are approaches to relax the non-convex optimization problems, their computational complexity is still a challenge . Moreover, the problem of path planning and obstacle avoidance for a humanoid robot can be viewed as a simplified dynamical system control approach, for example, by using potential fields .

2) Retargeting and Motion Generation

Given the continuous measurements from the teleoperation devices, we can divide the retargeting approaches into three groups: lower-body footstep motion generation, upper-body retargeting, and whole-body retargeting.

Lower-body footstep motion generation: The role of this block is to plan the footstep motion and find the sequence of foot locations and timings given the CoM position or velocity, and the floating base orientation or angular velocity provided by teleoperation devices. One possible approach to address this problem is based on the instantaneous capture point . Given the reference CoM position and velocity, one can compute the next foot contact point using the capture point relation in (3). In simple cases, the contact sequences can be preliminarily identified by the user for example by a finite state machine, and the desired footstep locations are modified to the left or right side of the capture point according to the nature of the foot contact (left or right). Another way to find the sequence of footsteps is to formulate an optimization problem, where the cost function is decided based on commonsense heuristics. The footstep timing can be found from the CoM velocity such that the total gait cycle duration corresponds to the average CoM velocity and gait length. This approach uses minimal information to generate footstep motion and does not enforce the user and the robot motion similarity.

Upper-body retargeting: In this method, the retargeting is done either in task space or configuration space. In the task space retargeting, the Cartesian pose (or velocity) of some human limbs is mapped to corresponding values for the robot limbs. Later, the inverse kinematic problem is solved by minimizing a cost function on the basis of the robot model while considering the robot constraints . Different authors considered disparate limbs as the target of the mapping. A popular approach is to map the motion of the human wrist to that of the robot end effectors . A commonly used mapping in the literature is to perform an identity map between the rotational motion of the human and the robot, whereas in the case of translational motion a fixed gain (due to differences in the geometry) is used . A more complicated approach may identify this rotational and translational gain as a function of the human intention and ongoing task. To enhance the similarity of the robot motion to the human one, the retargeting of the elbow motion with a lower priority in the optimization problem is suggested in . To overcome the manual morphing problem, suggested solving an optimization problem to identify geometric parameters of the morphing function.

Configuration space retargeting refers to the mapping in the joint space from human to robot. This morphing is normally used when the human and robot have similar joint orders. In this technique, human measurements and model are used in an inverse kinematics problem. The joint angles and velocity of the human joints are identified and mapped to the corresponding joints of the robot . When the human joint ranges differs from those of a humanoid, the robot constraints should also be applied in the morphing function.

Whole-body retargeting: This method measures the whole-body motion of human and kinematically retargets to the robot motion, similar to the upper-body retargeting approaches. Given the environment information, this approach may consider the contact constraints in the retargeting phase. Thus, this approach yields footstep locations, sequences, and timings. Later, outputs of this technique are provided to the stabilizer, to deliberate on the feasibility and enhance the robot stability . In , authors measured the normalized ground projection of human CoM from an arbitrary foot and retargeted it to the equivalent robot CoM ground projection, on a line connecting the two robot feet. This approach can be extended toward retargeting the heel-to-toe motion (orthogonal to the feet line) and multi-contact scenarios .

C. Stabilizer

The main goal of the stabilizer is to implement a control policy that dynamically adapt input references to enhance the stability and balance of the centroidal dynamics of the robot. Because of the complexity of robot dynamics, classical approaches are limited to examine the stability of a closed-loop control system. Therefore, other insights such as ZMP criteria and DCM dynamics are tailored in order to evaluate how far the robot is about to fall . The stabilizer gets inputs from the retargeting and planning level, as shown in Fig. 3. However, these reference trajectories may destabilize robot’s behavior, therefore the stabilizer adapts those references based on different criteria. Accordingly, the output of the stabilizer are references for the CoM position, the end-effector poses, joint angles, contact points, contact wrenches, and/or the rate of change of the momenta. Next, we provide an overview of stabilization approaches according to different criteria adopted so far in the literature.

Fig. 4: Different stability criteria approaches.

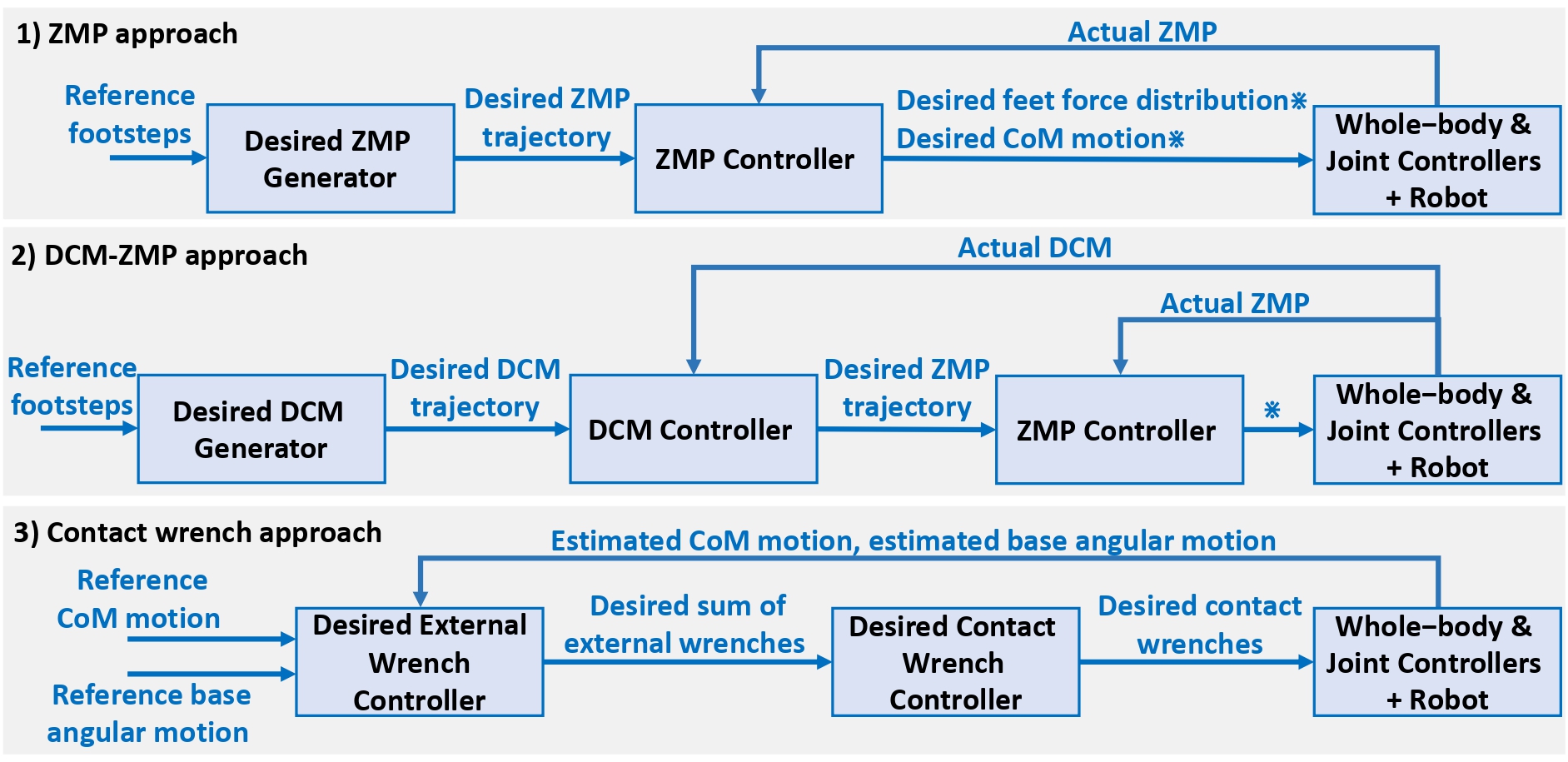
1) ZMP approach

This approach is based on the idea that the robot’s ZMP should remain inside of the support polygon of the base , as shown in Fig. 4. Given the footstep trajectories provided by the kinematic retargeting, this approach computes the desired ZMP. While walking, in single support the desired ZMP remains in the middle of the support polygon (e.g., left foot), and during double support the desired ZMP moves smoothly from the previous support leg to the middle of the new support polygon (e.g., from the left foot to the right foot). Following that, a ZMP controller makes sure that the real ZMP tracks the desired ZMP trajectory. However, the ZMP controller introduces several limitations. If the robot is subject to high disturbances, it does not adapt online to footstep locations to avoid the robot from falling. Moreover, this approach hardly extends to non-flat terrain or when the support foot rotates or slides.

2) DCM-ZMP approach

Another approach that is often employed with the simplified model retargeting and control is the DCM , which can be viewed as an extension of the capture point concept to the three-dimensional case for uneven terrain . Eq. 4 shows that the DCM dynamics is unstable, i.e., it has a strictly positive eigenvalue, and using equation of LIPM (2) it can be shown that the CoM dynamics converges to the DCM value. Therefore, the main goal of this controller is to implement a control law that stabilizes the unstable DCM dynamics (4) as well as the ZMP as mentioned previously. To stick to the formulation presented in Sec. III-A, the DCM-ZMP dynamic retargeting is explained with flat floor assumption; however, for the extension of the controller to 3D, one can refer to . The block diagram of the DCM-ZMP stabilizer is also shown in Fig. 4. DCM-ZMP approach has been deployed for whole-body retargeting in . In order to enhance the stability of the system, the authors have introduced the predicted support region where the time-delayed DCM of the robot is kept inside that region.

3) Contact wrench approach

This approach finds the desired contact wrenches at each contact point such that it enhances the robot stability. A schematic block diagram of this controller is shown in Fig. 4. This controller has been initially introduced in and later considered by as a stability augmentation criteria when introducing the contact constraints. This approach is similar to the momentum-based controller and will be explained in more detail later. However, to be thorough, we have mentioned it here as well.

D. Whole-Body Control Layer (WBC)

The WBC block in Fig.3 gets as input the retargeted human references corrected by the stabilizer, and provides as an output the robot joint angles, velocities, accelerations, and/or the joint torques. The whole-body control problem can be formalized with different cost functions and be solved as a QP problem or other approaches such as Linear Quadratic Regulator (LQR) and MPC . In the following, different whole-body control approaches are presented.

1) Whole-body inverse instantaneous velocity kinematics control

The problem of inverse instantaneous or velocity kinematics is to find the configuration state velocity vector \(\bf{\nu}(t)\) for a given set of task space velocities using the Jacobian relation. One common approach is to formalize the controller as a constrained QP problem with inequality and equality constraints. Conventional solutions of redundant inverse kinematics are founded on the pseudo-inverse of the Jacobian matrix .

2) Whole-body inverse kinematics control

The problem of Inverse Kinematics (IK) is to find the configuration space vector \(\bf{q}(t)\) given the reference task space poses. This problem can be sometimes solved analytically for determined robots; however, this solution is not scalable to different architectures and for a redundant humanoid robot (with a high degree of freedom), it is not feasible. Differently from inverse instantaneous velocity kinematics, to solve the IK problem a nonlinear constrained optimization problem is defined using the geometrical forward kinematics relation. Solving this problem might be time-consuming and the results can be discontinuous as well. To solve these challenges, a common approach in the literature is to transform the whole-body IK into a whole-body inverse velocity kinematics problem.

3) Whole-body inverse dynamics control

The Inverse Dynamics (ID) refers to the problem of finding the joint torques of the robot to achieve the desired motion given the robot’s constraints such as joint torque limits and feasible contacts. There are different techniques to solve the ID problem in the literature . To reach the desired end-effector poses and contact wrenches, one can formulate the ID problem as an optimization problem, minimizing the error on metrics such as the motion tasks and contact wrenches. Some of the constraints are dynamics equation of motion (1), joint angle, velocity, acceleration, or torque limits, collision avoidance constraints, and non-sliding contact constraints. The details of the constraints can be found in .

4) Momentum-based control

This controller finds the configuration space acceleration and ground reaction forces such that the robot follows the given desired rate of change of whole-body momentum . According to the Newton-Euler’s laws of motion and (1), the rate of change of centroidal momentum (the whole-body momenta of the humanoid robot about the CoM) is equal to the sum of all external wrenches applied to the robot. Using that, one can write the momentum-based controller in a QP fashion . Eventually, external wrenches and joint accelerations are used with an inverse dynamics algorithm to compute the robot joint torques.

E. Low-level Joint Controller

One of the main challenges in deploying a humanoid robot controller is the different behavior obtained in simulation and on the real robot of the low-level joint torque tracking. The low-level joint controller is in charge of generating motor commands to ensure the tracking of the higher-level control inputs. The input to the joint controller can be the desired joint positions, velocities, torques, or a mixture of them. The output of this controller is the current or voltage to the motors driving the joints. While the joint position can be directly measured by the encoder sensors, the joint velocity feedback is obtained by differentiating in time the encoder values, hence it can be noisy. Joint torque sensors or whole-body estimation algorithms equipped with distributed joint-torque sensors can estimate the generated joint torques. The torque control of the robot joints is more challenging because of the dynamics of the joints which are subject to friction and the mechanical power transmission from the motor to the joint shaft. On the other hand, compliance control of the joints allows for more robust locomotion and a safer interaction of the robot with the humans and the environment. For example, ankle joint torque control allows for conforming the foot to the ground in case of small obstacles or a mismatch between the ground slope and its estimation. However, the compliance control with only joint torques may lead to poor velocity or position tracking, therefore a mixture of them is proposed in the feedback and feed-forward terms of the joint controller in .

F. State Estimator, Localization and Mapping

These blocks in Fig. 3 receive measurements from the robot sensors and estimate the necessary information for other blocks in Fig.3 or to the human as shown in Fig. 2 (for assisted teleoperation). A family of well-known model-based estimation techniques commonly used in robotics is the Kalman filters. The joint encoders are used to estimate the joint angles, velocities, and acceleration. These joint states accompanied by the robot dynamics model in Eq. (1) and force/torque sensors can be used to estimate joint torques and external forces . To estimate the joint torques, the actuation system model can be learned or identified as well . If a humanoid robot is equipped with tactile sensors, the external wrenches and its point of application can be estimated likewise . To estimate the ground reaction wrenches and ZMP of a humanoid, its feet are normally equipped with force/torque sensors . Moreover, a combination of proprioceptive and exteroceptive sensory information allows a legged robot to estimate better the terrain characteristics and eventually elevate the control robustness . Finally, calculated joint angles and velocities are used to estimate the robot link poses and velocities through the forward kinematics. Combining those values with the robot link inertia, one can compute the CoM position and velocity . Moreover, considering the uncertainties of the link inertia and joint measurement noises, CoP and force/torque sensors are used to estimate CoM in .

One of the challenges specific to humanoid robots is the estimation of the robot base, and eventually robot localization in an environment. For the estimation, either proprioceptive sensors (i.e., joint encoders and IMU sensor attached to a robot link) or a combination of proprioceptive and exteroceptive sensors (such as cameras, GPS) are employed. When only proprioceptive sensors are used, a common approach is to assume that at each time instant at least one of the robot links is in contact with the ground, therefore the frame attached to the contact link has zero velocity and no slippage. With this assumption and taking into account the floating base frame pose in the kinematic chain, one can estimate the floating base velocity given the joint velocity vector, and eventually the base pose by integrating those velocities. However, the error of estimation is propagated over time due to kinematic modeling errors. To enhance the accuracy and limit the uncertainty of state estimation endowed with the odometry, IMU measurements are fused in the estimation process . Nevertheless, exploiting only the proprioceptive sensors does not lead to observability in the yaw axis (parallel to gravity vector) and the absolute position of the robot ; thereby exteroceptive sensors can facilitate to overcome this difficulty. Exteroceptive data such as camera information allows finding feasible regions for the humanoid robot foot locations as well as a map of the environment and obstacles.

G. Challenges and Future Directions for Retargeting and Control

Humanoid robot teleoperation is a new field, and many challenges to put together whole-body coordinated motion retargeting, planning, stability, and control are not addressed effectively yet. For example, dividing the retargeting and planning problems of humanoid robot teleoperations appears to be useful but not effective in performing agile teleoperation tasks outside of the lab (in the real world) and in unstructured environment as it is the case for many hazardous environments and disaster response scenarios. Many of the techniques adopted so far use simplified models of humanoid robots. Although these approaches are computationally efficient, they are limiting due to the adopted simplifying assumptions, e.g., fixed robot CoM height, ignorance of human or robot rotational motion, the existence of at least one contact point with no slippage between the robot and environment.

An alternative approach to solving simultaneously whole-body coordinated retargeting and planning problems is using the MPC technique and defining them as optimization problems with equality and inequality constraints. However, they are non-linear and non-convex optimization problems with large input and state spaces; therefore, they are computationally demanding, and the optimization may suffer from local minima. This issue intensified when retargeting the rotational motion and angular momentum of the human to the robot, while biomechanical studies show their importance as one major underlying component of the human-like coordinated motion . To this goal, an angular excursion index has been introduced by relating the whole-body orientation, angular velocity, and centroidal angular momentum. When this idea integrates with linear momentum, it enables highly agile motion with considerable rotational behaviors . However, retargeting the human angular excursion to the robot is an open problem. A possible trade-off solution between simplified and whole-body motion retargeting and planning approaches is to adopt the centroidal dynamics, the terrain map, and whole-body kinematics of the robot given the human measurements . This approach benefits from centroidal dynamics constraints and whole-body kinematics in collision avoidance and reachability computations. However, to adopt MPC in humanoid teleoperation scenarios, major challenges remain to predict future human motion and the difference between the surrounding terrain of human and robot.

While the MPC approach can be a valid solution for the humanoid robot teleoperation, it is not sufficient when deploying the robot in the real world to perform various tasks in an unstructured and dynamic environment with varying compliance and slippery characteristics. An approach to resolve these challenges is to introduce new sets of manual heuristics and constraints to the optimization problem for every scenario and environment. However, it is tedious and inefficient to generalize over different situations. To overcome these drawbacks, data-driven approaches with special attention to the robot dynamics and stability indications have shown promising results in the learning and mobile robot communities.

are some of the successful examples of leveraging neural networks and reinforcement learning (RL) techniques. In retargeting problems, safety considerations can be explicitly enforced as well . A novel approach blending an unsupervised learning technique with forward kinematics is proposed by . It relies on the cycle consistency principle, i.e., motions retargeted to the avatar should generate the original motions of the human when retargeted back. The general trend in whole-body planning of robots is that many robots simultaneously learn how to perform agile and dynamic motion robustly in a simulated environment, by incrementally introducing new complex terrain difficulties, dynamic obstacles, and terrain with different parameters. To relax the simulation to real-world gap, suggested learning robot actuator dynamics from the real robot and incorporating them with simulated robots. However, none of those works considered at the same time the whole-body coordinated motion retargeting of a human to a humanoid robot. We speculate that adding a reward term in an RL problem or using transfer learning techniques can impose the similarity of the human and humanoid robot motion during the training phase. While in some cases, human motion can be tracked by the humanoid robot, in other cases, the humanoid robot may perform step adjustments to keep its balance, for example, based on some behavioral selection techniques .